|
|
dimis
Responsible
Supreme Hero
Digitally signed by FoG
|
posted November 15, 2008 08:41 PM |
|
|
Quote:
Now that you have solved that one, can you solve the one with the Ls?
Wow, the chessboard had a very nice solution, and now I made it and proved the 6x6 board with the L's. Should I post solution? It's rather long though compared to the one-liner JJ gave for the chessboard. Thanks Ecoris, it was a really interesting problem! 
____________
The empty set
|
|
Asheera
Honorable
Undefeatable Hero
Elite Assassin
|
posted November 16, 2008 05:17 PM |
|
|
Sure, post it, I give up 
____________
|
|
dimis
Responsible
Supreme Hero
Digitally signed by FoG
|
posted November 16, 2008 05:24 PM |
|
|
Tetris-L's and 6x6 board
Ok, we have a 6x6 board => 36 squares.
I will color the squares of the board with 4 colors; name them A, B, C, and D in the following manner:
-------------------------
| A | B | A | B | A | B | ...
-------------------------
| C | D | C | D | C | D | ...
-------------------------
| A | B | A | B | ... .
----------------- .
| C | D | C | D | ... .
-----------------
| A | B | ... .
--------- .
| C | D | ... .
---------
. .
. .
. .
Therefore, I have
(eq. 1) 9 A's, 9 B's, 9 C's, and 9 D's.
Observe that once you place an L in a region it will cover twice one color and one time two other colors. Moreover, these two other colors, depend on the color that is covered twice.
Another thing that I am going to use is:
(average) If N numbers add up to X, then at least one of them is X/N (otherwise they sum up to something less than X)
These observations are enough for the proof.
So, how can I cover the entire board with L's? I have to cover twice some of the colors with each placement of L's.
First case - singletons: L's cover twice the same letter per placement => I have 2 squares per L * 9 L's = 18 squares with the same letter => eq. (1) is violated because I have exactly 9 squares with the same letter (color).
Second case - pairs: L's cover twice only one of two letters per placement. These two letters should cover 18 squares, meaning one of them should cover at least 18/2 = 9 squares. But hey ... these can be only multiples of 2, hence one of them should be at least 10. This contradicts eq. (1).
Third case - triples: L's cover twice only one of three letters per placement.
* Again, one of the letters should appear at least 18/3 = 6 times.
Say this is the maximum among all letters. There are 18-6 = 12 squares left to be split to the other two, so one of them should cover 12/2 = 6 squares, and since I assumed that 6 is maximum, this has to be 6 as well, which forces the other one to be 6 as well. Hence I have a triple (6,6,6). In that triple I necessarily find either the pair (A, B) or the pair (C, D). Say it is (A, B) - the argument is symmetric for (C, D). Then, I have 6 A's and the other 6 B's imply 3 more A's. By symmetry I have already covered 9 B's, since the 6 A's imply 3 more B's. So, the last 6 in the triple implies either 3 more A's, or 3 more B's. In either case you violate eq. (1).
* So, the maximum, can not be 6. Hence it should be 8 (7 is not a multiple of 2). Ok. If one of the three colors covers 8 squares, I have 18-8 = 10 squares to distribute to the other colors; i.e. one of them has at least 10/2 = 5 squares, which implies at least 6 (again you need a multiple of 2).
-- So I have the triple this time (8,6,4). Again, say the first one (8) belongs to A. Then 6 can not belong to B, since then, I get 3 more A's by that, which makes the A's 11 already contradicting eq. (1). Can 6 be C? No, because 6 C's imply 3 more A's, again contradicting eq. (1). So, it has to be that 6 represents the D's. But then, the 8 A's imply 4 B's and 4 C's, and the 6 D's imply 3 more B's and 3 more C's. So in total we have 7 B's and 7 C's. But then 4 has to be assigned to either B's or C's which again contradicts eq. (1).
-- Hence, 6 can not be the second maximum. What if it is 8? The triple this time is (8,8,2). Say the first one is A. Then we already have 8 A's, 4 B's and 4 C's. Hence, the second 8 can not represent B's or C's since it violates eq. (1). So it has to be a D again. However, 8 D's imply 4 more B's and 4 more C's. So in total we already have 8 B's and 8 C's. But then, the last 2 of the triple has to be assigned to either B's or C's, again contradicting eq. (1)
-- We concluded the triples, since the maximum can not be >= 10 by eq. (1).
Fourth case - quadruples: Therefore, all four colors should be covered by at least one L twice at some placement. The average this time is: 18/4 = 4.5 implying at least 5 squares which further implies 6 squares at least for the maximum.
-- First quadruple (6, 4, 4, 4). If 6 belongs to A, then 4 B's and 4 C's later on imply at least 2 + 2 = 4 more A's contradicting eq. (1).
-- Second quadruple (6, 6, 4, 2). If 6 is an A, then the second 6 is neither B nor C since it implies 3 more A's and you have an easy contradiction by the rest colors. So, the second 6 belongs to D. Then, A and D together imply 6 B's and 6 C's. But then, 4 has to be assigned to one of them, contradicting eq. (1) once again.
-- So the maximum should be at least 8. First quadruple under consideration is (8, 4, 4, 2). You already have 8 A's from 8, and at least one from the 2. But then, one of the two 4's implies 2 more A's, and ...
-- The next quadruple is (8, 6, 2, 2). Let 8 belong to A again. Then, if 6 belongs to B or C, you have 3 more A's; contradicts eq. (1). So, 6 belongs to D's. Then, the two 2's belong to B's and C's. Each one of them implies one more A, so in total you have 8 + 1 + 1 = 10 A's again contradicting eq. (1).
There are no more cases. Hence, you can not place the L's on the board and cover it exactly as we assumed.
Note, that by considering only A for the maximum in all the cases above, essentially I don't cheat. The reason is that if there is a placement of L's on a square board, this implies 3 more placements by rotating the tiling and leaving the board (and colors of the board) intact (the 4 corners of the board have different colors).
____________
The empty set
|
|
dimis
Responsible
Supreme Hero
Digitally signed by FoG
|
posted November 16, 2008 06:40 PM |
|
|
various
By the way, I am still expecting an IM with the b-days of the following guys/girls:
- Celfious -
- JollyJoker -
- Domzilla -
- JoonasTo -
- homm3megejas -
- Keldorn -
Please send a number from 1 to 366 to end this ...
And a question that comes along with a historical note. Can you prove that square root of two is irrational?
____________
The empty set
|
|
Asheera
Honorable
Undefeatable Hero
Elite Assassin
|
|
posted November 16, 2008 08:07 PM |
|
Edited by Asheera at 20:08, 16 Nov 2008.
|
Quote:
Can you prove that square root of two is irrational?
IIRC We have to take the case if sqrt(2) is rational, and then a contradiction comes.
I think it goes like this:
sqrt(2) = rational = a/b, a and b whole numbers, b not zero. Of course, a and b are simplified to the lowest terms.
Now, if we do the ^2 operation, we get: 2 = a^2/b^2  a^2 = 2 * b^2
So the square of a is an even number since it is two times something (which results in an even number ALWAYS)
From this we can also conclude that a itself is an even number, because an odd number multiplied by an odd number results in an odd number. So it can't be odd.
Since a is even, we can write a = 2x (two times something)
If we substitute a = 2x in the previous equation (2=a^2/b^2), we get 2 = (2x)^2/b^2
2 = 4x^2/b^2
2*b^2 = 4x^2
b^2 = 2x^2
This means the square of b is even, and this means b itself is even as well (see above with a)
Now, if both a and b are even, a/b can be simplified further, but we started assuming they are simplified to the lowest terms.
Contradiction => sqrt(2) can not be rational.
____________
|
|
dimis
Responsible
Supreme Hero
Digitally signed by FoG
|
|
posted November 16, 2008 09:19 PM |
|
Edited by dimis at 21:28, 16 Nov 2008.
|
Nice Asheera!
Now the historical note: The first proof of irrationality of square root of 2 was given by Pythagora. However, the proof is closely connected to another philosopher of that era; Ippasos (Metapontios) - in greek 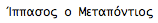 * - who was born around 500BC somewhere in Hellas (Greece). One variation of the story says that Ippasos was the first one who discovered the proof during a sea-trip, and pythagorean fanatics threw him into the sea. Another variation says that Ippasos revealed the proof to the public (i.e. outside the pythagorean club), something that led to his death sentence. The point is that pythagoreans had to give a vow of silence once entering the club. In any case though, this irrational number caused his death. It's a strange world ... I know ...
* The name is
Ίππασος ο Μεταπόντιος
and you can view the text by quoting this post.
____________
The empty set
|
|
JollyJoker
Honorable
Undefeatable Hero
|
|
posted November 16, 2008 09:57 PM |
|
|
|
Ecoris
Promising
Supreme Hero
|
|
posted November 17, 2008 10:38 AM |
|
|
Congratulations to dimis! Even though it's not a short one, a proof is a proof.
But if I ask you whether you can cover a 10x10 board with 25 Ls, what would you do? (You can apply the same procedure. You will only have to consider the same four cases, but each of those will have many more subcases, e.g. in the fourth case one would have to consider (24,22,2,2), (24,20,4,2), (24,18,6,2), (24,18,4,4), ... etc. And then I could ask whether a 14x14 board could be done).
I don't have a one-line solution, but I may be able to do it in three lines. Should I post the solution?
____________
|
|
TitaniumAlloy
Honorable
Legendary Hero
Professional
|
|
posted November 17, 2008 10:52 AM |
|
|
I finished all my maths exams now.
Overall I did better than I thought I would - I finished the Specialist exam, which I didn't expect to, and the easier ones I found pretty easy. Go figure.
Anyway one memorable question that stumped me, which I immediately realized after is actually ridiculously easy, was this:
What is the area under the graph from -1 < x < 1?
I over thought it
(edited out answer)
My b.
Good thing that it was only worth 1 or 2 marks, and I got the followup questions.
|
|
dimis
Responsible
Supreme Hero
Digitally signed by FoG
|
|
posted November 17, 2008 02:09 PM |
|
|
@Ecoris: Give us some time. These days are like crazy.
@TA: I think you helped a lot. 
____________
The empty set
|
|
Gnoll_Mage
Responsible
Supreme Hero
|
|
posted November 17, 2008 02:59 PM |
|
|
My tiling problem:
Suppose I have a square grid-board whose sides are a multiple of two. I then specify a single square of that grid arbitrarily. Prove that it's always possible to cover all of the board, except that square, with
X X
X
shapes.
|
|
Gnoll_Mage
Responsible
Supreme Hero
|
|
posted November 17, 2008 03:01 PM |
|
|
|
Ecoris
Promising
Supreme Hero
|
|
posted November 17, 2008 04:40 PM |
|
Edited by Ecoris at 16:41, 17 Nov 2008.
|
Quote:
My tiling problem:
Suppose I have a square grid-board whose sides are a multiple of two. I then specify a single square of that grid arbitrarily. Prove that it's always possible to cover all of the board, except that square, with
X X
X
shapes.
You can't cover a 6x6 board with a single square removed; that leaves 35 squares and 35 is not divisible by 3.
But it is easy to prove that you can make such a cover if the side length is a power of 2.
____________
|
|
dimis
Responsible
Supreme Hero
Digitally signed by FoG
|
posted November 17, 2008 10:52 PM |
|
|
Tetris L's revisited
Ok, we can state the following:
(theorem) If the board is (2*(2k+1)) x (2*(2k + 1)), then we can not cover the board with tetris L's.
(i.e. 6x6 is the smallest for k = 1)
Proof: The size of the board implies 2^2(2k+1)^2 = 4(4k^2 + 4k + 1) squares, which means that we have to use 4k^2 + 4k + 1 = 4(k^2 + k) + 1 tetris L's. So we have TWO very important observations:
(OBSERVATION 1) Each letter occupies 4k^2 + 4k + 1 squares ==> ODD number of squares.
(OBSERVATION 2) We are going to use 4k^2 + 4k + 1 tetris L's ==> ODD number of tetris L's.
Again we color the board as I did above, and characterize the tetris L's according to the color they cover twice. Say there are 'a' L's that cover A's twice, 'b' L's that cover B's twice, 'c' L's that cover C's twice, and 'd' L's that cover D's twice.
By obs. 2: a + b + c + d = ODD
But four numbers add up to something ODD only in TWO possible ways ...
First case - (even, even, even, odd):
Say that a is even and b, c are even too. Since the d's do NOT imply A's, the A's are (2*a) + b + c = even + even + even = even ==> contradiction to observation 1.
So, d can not be odd. Make it even. Say c will be odd now.
Then, a, d, and b, are all even and imply an even number of B's (since the c's this time never "produce" a B). Again contradiction.
The argument is symmetric if b is odd. No more cases.
Second case - (even, odd, odd, odd):
Assume a is even again. Then an odd number of b's and c's (these are tetris L's, remember?) implies an EVEN amount of A's. Plus the even amount of A's that we have by the even 'a', again we have even A's. Contradiction to observation 1.
This concludes the proof.
As I said earlier, I don't cheat by first fixing A and then the rest. However, it is obvious I think that the argument is cyclic no matter which letter one fixes first.
Now I am happy. 
____________
The empty set
|
|
dimis
Responsible
Supreme Hero
Digitally signed by FoG
|
|
posted November 18, 2008 05:59 AM |
|
Edited by dimis at 06:25, 18 Nov 2008.
|
Just to clarify something that wasn't stated correctly earlier.
Real numbers as a set have higher cardinality than integers as a set.
I just want to stress this, since real algebraic numbers have the same size as integers.
What are real algebraic numbers? Any rational or irrational solution of a polynomial with integer coefficients. For example, square root of 2, fifth root of 3, square root of 2 + fifth root of 3, and so on, are real algebraic numbers.
--- /parenthesis
How many real numbers do we learn at school that are NOT real algebraic numbers? I guess only two: e ~= 2.718281828459045 ... and \pi ~= 3.14159265...
HOWEVER, the above statement says that irrationals that are not real algebraic are waaaaay more. Hmmm ... how many did we learn at school?
To put it in an even other way: Suppose you have the interval [0,1] and you pick a number from that interval at random. Then with probability 1 you 'll pick a number that is neither integer, nor rational, not EVEN real algebraic ... amazing ?
--- /end of parenthesis
Why are they enumerable? Because the polynomials that "produce" them are enumerable. Why the polynomials are enumerable? Because essentially you can describe a polynomial by it's coefficients, which are integers and hence enumerable.
If someone wants I can elaborate more. I just wanted to make this clarification.
Any takers on TA's problem? Or should I post my guess after some long integration?
____________
The empty set
|
|
Gnoll_Mage
Responsible
Supreme Hero
|
|
posted November 18, 2008 10:26 AM |
|
|
|
I don't understand observation one...
|
|
Lord_Pc
Promising
Famous Hero
Groin-Grabingly Clever
|
|
posted November 18, 2008 02:12 PM |
|
|
I'll take a guess at TA's and guess say pi
I dont think I could work it out mathematically [if someone could integrate x / (1-x^2)^(1/2) that would help me out to do so]
But if you look at it geometrically I would say it is just as good, if not much more simpler
the inverse cos graph has half turn symmetry or rotational symmetry or whatever you want to call it, about the point (0, pi/2) and by integrating we would want to find the red area (see below)
but then if we use the symmetry of the graph, we can see that the two sections, from -1 to 0 and from 0 to 1 make a rectangle with dimensions pi and 1. therefore the area of the rectangle is pi, hence the area under the graph is pi.
____________
Da-da-dada-HEY-dada-da-da
Two goldfish were in their tank. One turns to the other and says, 'You man the guns, I'll drive.'
|
|
TheDeath
Responsible
Undefeatable Hero
with serious business
|
|
posted November 18, 2008 02:17 PM |
|
Edited by TheDeath at 14:18, 18 Nov 2008.
|
Quote:
To put it in an even other way: Suppose you have the interval [0,1] and you pick a number from that interval at random. Then with probability 1 you 'll pick a number that is neither integer, nor rational, not EVEN real algebraic ... amazing ?
--- /end of parenthesis
Not really amazing since you have infinite numbers there
EDI: Nevermind about the rest I missed something 
____________
The above post is subject to SIRIOUSness.
No jokes were harmed during the making of this signature.
|
|
dimis
Responsible
Supreme Hero
Digitally signed by FoG
|
|
posted November 18, 2008 02:18 PM |
|
Edited by dimis at 14:35, 18 Nov 2008.
|
Quote:
I don't understand observation one...
Ok. The board has length on each side 2*(2k + 1), so, in total we have ( 2*(2k + 1) )^2 squares; i.e. we have 4*(4k^2 + 4k + 1) squares. The way we color the board we distribute the squares evenly among all 4 letters. So, each letter is just the quarter of 4*(4k^2 + 4k + 1); hence it is 4k^2 + 4k + 1.
Why this is odd? 4k^2 + 4k + 1 = 4(k^2 + k) + 1 = four times something plus one = even plus one = odd
@TheDeath: The fact that you have infinite numbers doesn't imply anything. The rationals in that interval are infinite, not to mention all the real algebraics in that interval; e.g. the numbers sqrt{2} / 2, sqrt{2}/3, ... also appear, but you have NO CHANCE of selecting such a number.
[But with probability 1 you 'll pick a number that is *not* real algebraic]
Anyway, that was counter intuitive to me a few years back, that's why I mention it.
May be what you want is a way to express non-zero probability. You can ask what is the probability for a number to lie in e.g. 1/10 of that interval. Then the probability is 1/10 ...
Quote:
Or should I post my guess after some long integration?
I am with you LordPC on pi, and that line was meant to be a joke, but it could have been a bad one had I added a in the end. Now, that someone has observed it, I can add it safely! So there
____________
The empty set
|
|
Ecoris
Promising
Supreme Hero
|
|
posted November 18, 2008 05:50 PM |
|
Edited by Ecoris at 17:57, 18 Nov 2008.
|
Now that dimis had improved his proof to cover the general case (it's also a lot nicer to read) I'll give a short proof too:
Color every second column black and the other ones white (3 columns of each color). Then any L covers 3 black squares and 1 white square, or 3 white squares and 1 black square. We have to place 9 Ls so they will cover an odd number of black tiles, but there are 18 black squares on the board.
The same argument holds for boards of dimension (4k+2)x(4k+2) since such boards require an odd number of Ls.
@ gnollmage
Could you revise your problem?
The real algebraic numbers mentioned by dimis form a field. Can anyone prove this?
(You have to show that the product or sum of two algebraic numbers is again an algebraic number, and that if x is a non-zero algebraic number then 1/x is too).
____________
|
| |
|
|
This thread is pages long: 
