|
|
dimis

   
    
Responsible
Supreme Hero
Digitally signed by FoG
|
 posted May 27, 2010 01:52 PM
posted May 27, 2010 01:52 PM |
|
|
FoG, I am happy that you are happy with Risk! 
Regarding Q17, half of 324,000.
Mytical,
when you give a real problem, please copy-paste the problem and do not write it down in your own words. In particular the answer that you agreed earlier has a problem; 90% of the class has written scores above (about) 90/100, and yet you end up with an average around 80/100. This is strange since you could achieve it only if the rest 10% writes 0/100. Hence (0.9 * 0.9 =about= 0.8)
Finally, I am not a mathematician of any kind. I work in Computer Science.
____________
The empty set
|
|
Corribus


Hero of Order
The Abyss Staring Back at You
|
 posted May 27, 2010 03:24 PM
posted May 27, 2010 03:24 PM |
|
|
@dimis
Quote:
Regarding Q17, half of 324,000
That's correct -> want to share how you got the answer?? 
You want to post a Q18?
____________
I'm sick of following my dreams. I'm just going to ask them where they're goin', and hook up with them later. -Mitch Hedberg
|
|
dimis

   
    
Responsible
Supreme Hero
Digitally signed by FoG
|
 posted May 27, 2010 03:41 PM
posted May 27, 2010 03:41 PM |
|
Edited by dimis at 15:44, 27 May 2010.
|
Yes, the sequence 1, 1, 2, 9, 96, 2500.... was the product of different lines of the pascal-triangle
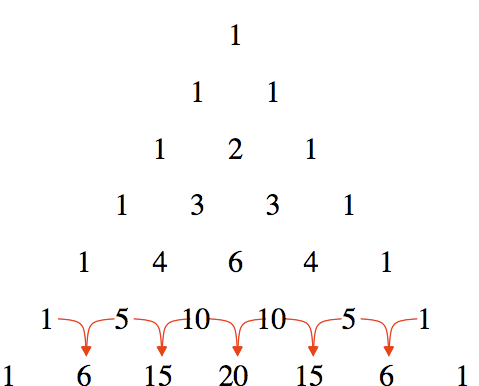
Each line of the pascal triangle is obtained by the previous one in the sense that each entry is the sum of the two numbers in the above row.
I will come back with a question for Q18, but these days I am not going to be regular, so feel free to post more problems.
____________
The empty set
|
|
Corribus


Hero of Order
The Abyss Staring Back at You
|
 posted May 27, 2010 03:44 PM
posted May 27, 2010 03:44 PM |
|
|
Yes that's where the sequence comes from - I was just curious why you expressed it as "half of 324000".
____________
I'm sick of following my dreams. I'm just going to ask them where they're goin', and hook up with them later. -Mitch Hedberg
|
|
dimis

   
    
Responsible
Supreme Hero
Digitally signed by FoG
|
 posted May 27, 2010 03:45 PM
posted May 27, 2010 03:45 PM |
|
|
Playing with words I guess ... 
____________
The empty set
|
|
dimis

   
    
Responsible
Supreme Hero
Digitally signed by FoG
|
 posted May 27, 2010 03:50 PM
posted May 27, 2010 03:50 PM |
|
|
Q18. Confusion.
The son of a professor's father is talking to the father of the professor's son, and the professor does not take part in the conversation. Is this possible ?
____________
The empty set
|
|
alcibiades

    
      
Honorable
Undefeatable Hero
of Gold Dragons
|
 posted May 27, 2010 05:22 PM
posted May 27, 2010 05:22 PM |
|
|
Well if the professor is female, it would be?
____________
What will happen now?
|
|
dimis

   
    
Responsible
Supreme Hero
Digitally signed by FoG
|
 posted May 27, 2010 05:38 PM
posted May 27, 2010 05:38 PM |
|
|
Yes. You were fast! 
____________
The empty set
|
|
ihor

 
    
Supreme Hero
Accidental Hero
|
 posted June 02, 2010 09:07 PM
posted June 02, 2010 09:07 PM |
|
|
Q19.
Time for a new puzzle.
Q19. You have a sequence {a} with following properties:
a_1 = 1
a_2 = 2
a_3 = 3
For every positive integer n:
a_n+3 = a_n + a_n+1 - a_n+2
What is the value of a_2010 ?
|
|
Corribus


Hero of Order
The Abyss Staring Back at You
|
 posted June 04, 2010 08:17 PM
posted June 04, 2010 08:17 PM |
|
|
I'll give this one a guess: -2006
I used a stupid way to do it so I'll not be surprised if I'm wrong. 
____________
I'm sick of following my dreams. I'm just going to ask them where they're goin', and hook up with them later. -Mitch Hedberg
|
|
Zenithale

  
   
Promising
Famous Hero
Zen Mind
|
 posted June 04, 2010 09:16 PM
posted June 04, 2010 09:16 PM |
|
|
|
ihor

 
    
Supreme Hero
Accidental Hero
|
 posted June 05, 2010 08:06 PM
posted June 05, 2010 08:06 PM |
|
|
Yes, thats correct. That was one which is easy to guess for everyone.
Method of mathematical induction is suitable for clean proof.
|
|
Corribus


Hero of Order
The Abyss Staring Back at You
|
 posted June 05, 2010 09:43 PM
posted June 05, 2010 09:43 PM |
|
|
I used Excel. 
____________
I'm sick of following my dreams. I'm just going to ask them where they're goin', and hook up with them later. -Mitch Hedberg
|
|
ihor

 
    
Supreme Hero
Accidental Hero
|
 posted June 05, 2010 11:05 PM
posted June 05, 2010 11:05 PM |
|
Edited by ihor at 23:06, 05 Jun 2010.
|
  
I should have written to find a_10000000.
|
|
dimis

   
    
Responsible
Supreme Hero
Digitally signed by FoG
|
 posted June 08, 2010 12:46 PM
posted June 08, 2010 12:46 PM |
|
|
Q20. Comparing Numbers
Which number is greater: 2^{300} or 3^{200} ?
____________
The empty set
|
|
ohforfsake

  
     
Promising
Legendary Hero
Initiate
|
 posted June 08, 2010 05:12 PM
posted June 08, 2010 05:12 PM |
|
|
I wonder if it can be generalized. Anyway for the specific case:
let X be any given number that is defined as:
X * 2^(300) = 3^(200)
Now if X > 1, 3^(200) is bigger, if X = 1, they're the same, and if X < 1, 3^(200) is smaller.
Using that 2^(300) = 2^(200)*2^(100):
X * 2^(200)*2^(100) = 3^(200)
X * 2^(100) = 1.5^(200)
X * (4/3)^(100) = 1.5^(100)
Since 4/3 < 1.5 it follows that X > 1 and thereby 3^(200) > 2^(300)
Though I think this method is only useable when the numbers go up in each other a finite amount of times. I wonder if it is possible to do like this, with numbers that continue infinitely, like 1/3th.
____________
Living time backwards
|
|
Warmonger

  
     
Promising
Legendary Hero
fallen artist
|
 posted June 08, 2010 05:22 PM
posted June 08, 2010 05:22 PM |
|
|
Quote:
Which number is greater: 2^{300} or 3^{200} ?
Can we use logarithms? 
Alternatively I would compare (2^3)^100 and (3^2)^100. Obviously the second one is greater, as 9>8.
____________
The future of Heroes 3 is here!
|
|
ohforfsake

  
     
Promising
Legendary Hero
Initiate
|
 posted June 09, 2010 08:15 PM
posted June 09, 2010 08:15 PM |
|
|
So I thought about it a little more. I suppose you can always write any number, b, as the product of d and e, so:
X*a^b=c^d = a^(e*d), which means you get:
X*a^e = c
Though not sure on how to continue on from there, in the previous example, it'd be ending at comparing 2^(3/2) with 3, or sqrt(8) with 3 if you want.
____________
Living time backwards
|
|
Corribus


Hero of Order
The Abyss Staring Back at You
|
 posted June 12, 2010 06:24 AM
posted June 12, 2010 06:24 AM |
|
|
Q21. Friend or No Friend?
A friend of yours visits you and asks if you would like to play a card game. The card game works as follows. He deals four cards from a standard deck of cards onto a table. If the four cards are the same suit, he pays you one dollar. If the four cards are one of each suit, you pay him one dollar. If the four cards are any other arrangement of suits, you both keep your money.
Should you play?
|
|
friendofgunnar

    
     
Honorable
Legendary Hero
able to speed up time
|
 posted June 14, 2010 01:39 AM
posted June 14, 2010 01:39 AM |
|
|
Q22. OhforSake's Tuesday problem reprinted:
Quote:
The tuesday problem and when no analytical solution exists.
So first the tuesday problem. It goes like this:
The chance of getting a boy is 50%, the possible outcomes are either a boy or a girl. A person have two kids. One of them is a boy. One of them are born on a tuesday. What are the chances the second kid is a girl?
So, the answers should be 14/27 for the second being a girl if you know it's on a tuesday the boy is born and if you don't know what day of the week, then the chance is 2/3 for the second being a girl.
Now, I don't really agree with this. As I see it, the chance is either 1 or 0, because this person already have two kids, the event already happened. On the other hand, had the question been, if you were to guess what gender my other kid is based on information X, then I'd agree with the probabilities given.
I think people automatically thinks the situation is there's one unborn child and then needs to find the probability of the unborn child being a girl, but if one child was unborn, then the chance would be 50% girl/boy and the day of the week wouldn't matter, I think, because now it's not "one is a boy", no it's "the first one is a boy".
This makes all the difference!
Let me illustrate:
If you know nothing, except for two kids, the possibilities are:
GB, BG, BB, GG. [It means, first kid girl, second boy, etc.]
A) If you know the first one is a boy, the possibilities are:
BG, BB.
B) If you know one of the two is a boy, the possibilities are:
BB, GB, BG. [In reality, there's only one possibility, because the outcome has already happened].
So for case A) it's 50/50 and for case B) it's 2/3 for girl and 1/3 for boy, if you were to guess. [Again, it has already happened, case B) is merely finding out the best thing to guess for, not what is the most likely child to be born, because childs are born in a differentable order, kid 1, kid 2. In the case of case B) however you can't seperate kid 1 and kid 2 and therefore have to count both cases].
Now adding the weekday information. If we go back to case A), where you know the first is a boy, the weekday makes no difference, because the possible outcomes becomes:
Boy burn on tuesday followed by boy born some day contra girl born some day. The day, tuesday, does not change the possible outcomes of the second child.
However, in the case of the child already been determined and therefore you don't know if it's the first or second child you've information about, the information of the weekday changes the chances of guessing correct. It's because the weekday information limits the possible outcomes, like this:
Either it's BG:
Then the boy is born a tuesday and the girl in one of the seven weekdays (7 possibilities).
Or it's GB:
Then the boy is born a tuesday and the girl in one of the seven weekdays (7 possibilities).
Or it's BB, however before BB only occured in one way (whereas GB and BG occoured in twice as many ways, which is still true, if the boy could have been born on any given day of the week, which I'll show in a moment), now it occours in many ways:
One way is Boy born on tuesday, followed by boy born any weekday (7 possibilities), the other being boy born on any weekday, followed by boy born on a tuesday (now 6 possibilities, because tuesday/tuesday is already counted). In total this gives 27 possibilities and the chance of a girl is 7+7, which means the tuesday information changes the outcome of you guessing correct, if you guessing a girl to 14/27 in stead of 2/3.
So let's look at the boy being born on any given day of the week, as I said I would:
Boy born on any day, followed by girl born on any day. The possibilities are 7*7, 49.
Next, girl born on any day, followed by boy born on any day, again 49 possibilities.
Now for BB, there are boy born on any day, followed by boy born on any day, the possibilities are:
7*7=49 possibilities.
The difference lies in, that the tuesday information for case A) did not remove any possible outcomes, it did for case B), where there's no difference for the girl outcomes, for the boy outcome, the following possibilities can be listed:
MM
MT
MW
MT
MF
MS
MS
TM
TT
TW
TT
TF
TS
TS
WM
WT
WW
WT
WF
WS
WS
TM
TT
TW
TT
TF
TS
TS
FM
FT
FW
FT
FF
FS
FS
SM
ST
SW
ST
SF
SS
SS
SM
ST
SW
ST
SF
SS
SS
Now, for case A), that list goes down to 7 possibilities, because you know the first one is a boy [on a tusday, so all starting with a T (that is not thursday)], and so the possible days for a girl also goes to 7 possibilites. However for case B), the list changes from all those 49 possibilities, with no information about the weekday, to all that contains a tuesday, when the information about tuesday is added, and that is in total 13 possibilities that contains a tuesday:
MT
TM
TT
TW
TT
TF
TS
TS
WT
TT
FT
ST
ST
This does however seem counter intuitive. So you're to guess if the second kid is a girl or a boy and wants to find out what is the best guess, i.e. what guess gives you the right answer most times. You know that one of the kids is a boy, and you know that the boy is born on a given day of the week, it might as well be tuesday, it might be any day of the week though. So it does seem weird that getting told it's a tuesday should alter the information, would a proper way of dealing with the problem not be to assume the boy is born on a given weekday in the first place, realise that there's no difference what weekday is choosen [it always goes from 49 to 13 possibilities] and then choose one at random? For yes, the boy could be born on any given day of the week, but no matter what day you're told, the boy is born on one of those days, which means all other possibilities becomes impossible to the degree of assumptions put on the system and therefore, I'd think, should not be counted.
So to me, it seems like, the initial question, the one without information about the day "I have two kids, one is a boy, if you guess girl, what are the chances you guess correct", does not take into consideration that the boy already is born on a given day and is not going to be born on a certain day. Therefore, I'd say no matter the information of birth on a tuesday, the probability should be 13/27 for boy, 14/27 for girl. Heck maybe there are even more assumptions that should be added, more information, and maybe it actually is 50/50?
What I mean is that in the BG/GB/BB Scenario, it's assumed that BG,GB and BB are picked equally often, but looking through the weekdays they can be born and knowing the boy is born on a given weekday, it reduces it to a 13/27 contra 14/27 probability for guessing correct, not a 1/3 contra a 2/3.
Then again, if one takes into account that one knows the other child, boy or girl, is born on a given weekday as well, then for born on a tuesday it becomes 1/3 contra 2/3 and for all other days it becomes 50/50.
Hmm, I'm confused, hopefully someone can make it more clear.
Now to the next thing I have been thinking about. I have often been told there are equations of which there are no analytical solution. To which I wonder, is that not simply because we don't have a set of functions to describe any possible curve. I'd guess if we'd a set of functions that could describe any possible curve, then we could solve every equation analytical. I'd guess so because every solution to a given equation always is in the form of a given n-dimensional curve, to my knowledge. If we had a set of functions that could describe any curve, then the right combination of these functions would always be able to create such a curve, in return meaning that the solution is analytical, I'd think.
The type of functions I know about are, to my knowledge, not designed due to any geometrical advantages, these functions are those general from operations such as sum, product (which basicly just is a more generalized way of sum, I believe), and potens/exponent (which basicly is just a more generalized way of product, I believe). Then there are the sinus and cosinus functions which are closely related to the exponent functions through imaginable numbers, which in return means, if one expands the set of possible input numbers to imaginary, these functions are as well part of the exponent functions, a^x.
However, as it is, to my knowledge, no combination of any of these types of functions can describe a sharp change in a curve, like what I try to draw below:
/
___/
This could be described as the function y = k [k is constant] from x = a to x = b, where a and b are some numbers.
And y = x for x = b to x = c, where b and c again are some numbers.
But the unified function from a to c can, to my knowledge, not be described through the means of any of those functions I listed. Though, I can imagine, a fourier transformation could maybe bring one very, very, close, since I specified a closed area, but if the functions were global (-infinity to b,y=k and b to infinity,y=x). I'd imagine a set of functions designed to describe any type of geometrical shape/curve in a n-dimensional space would on the other hand be able to solve this problem. Though then there's of course, when going from curve, to shape, the whole problem of several y-values for a single x-value (like the squareroot of any non-zero number provides two possible outcomes, Y and -Y). Though if at least every possible curve where described, then every equation would have an analytical solution, I'd guess. [Maybe it already has, just only approximative? As mentioned with the fourier transformation, one can expand a function in a potens base (taylor), or maybe a exponential base (fourier) and then solve for the function in the local region, but the approximation, not only have some assumptions needs to be meet, (like I believe the taylor expansion requires the function to be differentiable in every single point), but will always be approximative [as it gets closer and closer to the given region of space selected] and therefore, not really useable, if you want to know what happens values of x's far away (I'm not sure, is this where chaos theory originates from?). So all in all, I think it'd be pretty nice with such a set of functions that could describe any possible curve in an n-domensional space.
This was actually an interesting problem because I sensed intuitively that Ohfor wasn't phrasing the problem correctly. There was some witchy odds in there but I had to disentangle them from the way they were stated. This statement was particularly confusing for everything that came after it. "A person have two kids. One of them is a boy. One of them are born on a tuesday. What are the chances the second kid is a girl?
I'll take this step by step.
"A couple has two kids. One is a boy."
The statement "The other is a girl" will be correct 2/3 of the time.
"A couple has two kids. One is a boy. One was born on tuesday."
The statement "The other is a girl" will be correct 2/3 of the time. (The tuesday information is irrelevant here)
"A couple has two kids. One is a boy who was born on tuesday."
I'm going to modify this statement a bit:
"A couple has two kids. At least one is a boy who was born on tuesday."
Here's all the possible combinations: (the number represents the day of the week the person was born)
two boys
11 12 13 14 15 16 17
21 22 23 24 25 26 27
31 32 33 34 35 36 37
41 42 43 44 45 46 47
51 52 53 54 55 56 57
61 62 63 64 65 66 67
71 72 73 74 75 76 77
girl and a boy
11 12 13 14 15 16 17
21 22 23 24 25 26 27
31 32 33 34 35 36 37
41 42 43 44 45 46 47
51 52 53 54 55 56 57
61 62 63 64 65 66 67
71 72 73 74 75 76 77
boy and a girl
11 12 13 14 15 16 17
21 22 23 24 25 26 27
31 32 33 34 35 36 37
41 42 43 44 45 46 47
51 52 53 54 55 56 57
61 62 63 64 65 66 67
71 72 73 74 75 76 77
two girls
11 12 13 14 15 16 17
21 22 23 24 25 26 27
31 32 33 34 35 36 37
41 42 43 44 45 46 47
51 52 53 54 55 56 57
61 62 63 64 65 66 67
71 72 73 74 75 76 77
Now we disallow anything that is not possible under this statement "At least one is a boy who was born on tuesday.":
two boys
11 12 13 14 15 16 17
21 22 23 24 25 26 27
31 32 33 34 35 36 37
41 42 43 44 45 46 47
51 52 53 54 55 56 57
61 62 63 64 65 66 67
71 72 73 74 75 76 77
girl and a boy
11 12 13 14 15 16 17
21 22 23 24 25 26 27
31 32 33 34 35 36 37
41 42 43 44 45 46 47
51 52 53 54 55 56 57
61 62 63 64 65 66 67
71 72 73 74 75 76 77
boy and a girl
11 12 13 14 15 16 17
21 22 23 24 25 26 27
31 32 33 34 35 36 37
41 42 43 44 45 46 47
51 52 53 54 55 56 57
61 62 63 64 65 66 67
71 72 73 74 75 76 77
two girls
11 12 13 14 15 16 17
21 22 23 24 25 26 27
31 32 33 34 35 36 37
41 42 43 44 45 46 47
51 52 53 54 55 56 57
61 62 63 64 65 66 67
71 72 73 74 75 76 77
As you can see, there's 27 possibilites left, of which there's 14 where this statement "The other is a girl" is true. So the odds are 14/27.
Let's now change the statement to this: "Only one is a boy who was born on tuesday." The important thing about this statement is that it disallows the possibility that there were two boys that were born on tuesday.
two boys
11 12 13 14 15 16 17
21 22 23 24 25 26 27
31 32 33 34 35 36 37
41 42 43 44 45 46 47
51 52 53 54 55 56 57
61 62 63 64 65 66 67
71 72 73 74 75 76 77
girl and a boy
11 12 13 14 15 16 17
21 22 23 24 25 26 27
31 32 33 34 35 36 37
41 42 43 44 45 46 47
51 52 53 54 55 56 57
61 62 63 64 65 66 67
71 72 73 74 75 76 77
boy and a girl
11 12 13 14 15 16 17
21 22 23 24 25 26 27
31 32 33 34 35 36 37
41 42 43 44 45 46 47
51 52 53 54 55 56 57
61 62 63 64 65 66 67
71 72 73 74 75 76 77
two girls
11 12 13 14 15 16 17
21 22 23 24 25 26 27
31 32 33 34 35 36 37
41 42 43 44 45 46 47
51 52 53 54 55 56 57
61 62 63 64 65 66 67
71 72 73 74 75 76 77
In this case there's 26 possibilites left, of which there's 14 where this statement "The other is a girl" is true. So the odds are 7/13.
The reason this question is so hard is because of the ambiguity in this statement: "One is a boy who was born on tuesday."
From a strictly logical standpoint this means "Only one is a boy who was born on tuesday." However in common usage when we hear this statement: "One is a boy who was born on tuesday." we tend to think "At least one is a boy who was born on tuesday"
|
| |
|
|





