|
|
friendofgunnar
Honorable
Legendary Hero
able to speed up time
|
posted November 10, 2008 07:10 AM |
|
|
Quote:
But for the third person to have a 363/365 chance as stated, that would be assuming that the first two do NOT share the same birthday, right?
I'm not sure how to fix this. Would it be (363+1/365)/365? Or maybe 363/365 * (1+1/365)? My guess is the former.
If you were trying to figure out the chances of two people having the same birthday but not three or more people sharing the same birthday you would have to start adding in little fractions and whatnot like you suggest. But as it is, you're only trying to figure out the minimum chances of at least two people having the same birthday.
In regards to Ecoris's question (hmmm, an english question just suggested itself: should it be "Ecoris' question"?)
If you multiply the first one hundred numbers together 1 * 2 * 3 *...* 100, you'll get the first number of Ecoris' series, because any number within the next 100 numbers will be guarenteed to be a multiple of one of the first 100 numbers.
There's another 100 consecutive numbers much smaller than that though.
And here's another question, is there a way to prove that there's no 100 consecutive numbers smaller than that second series?(the one that I didn't give an answer to)
|
|
Asheera
Honorable
Undefeatable Hero
Elite Assassin
|
|
posted November 10, 2008 01:58 PM |
|
|
Quote:
Oh, please, can the participants send me an email/im with their birthday (not year)? Let's see which side of the coin we are facing ... 
You could look here for a start, although it doesn't have all the participants in this thread I think...
____________
|
|
TheDeath
Responsible
Undefeatable Hero
with serious business
|
|
posted November 10, 2008 02:04 PM |
|
|
Ok i re-thought the process and now my solution seems very wrong, I'm sorry for that 
This is because, when I took 4 people having the same birthday, it only happened if all 4 shared the same day, not for example 2 on a day and 2 on another one (which is still valid). Sorry for my mistake.
____________
The above post is subject to SIRIOUSness.
No jokes were harmed during the making of this signature.
|
|
Asheera
Honorable
Undefeatable Hero
Elite Assassin
|
|
posted November 10, 2008 03:25 PM |
|
|
Quote:
i found this on the net...
can someone explain before my brain hemorrhages
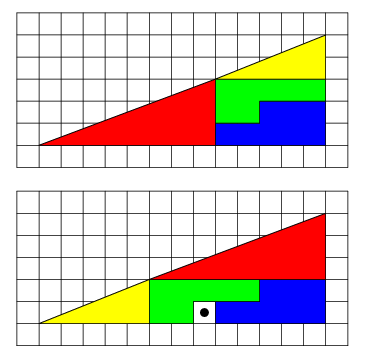
Red Triangle has the hypoteneuse = sqrt(8*8 + 3*3) = sqrt(73)
Yellow Triangle has the hypoteneuse = sqrt(5*5 + 2*2) = sqrt(29)
The whole big triangle would have a hypoteneuse = sqrt(13*13 + 5*5) = sqrt(194)
Red's hypoteneuse + Yellow's hypoteneuse should be equal to the big triangle's hypoteneuse. But it's NOT. Close, but not equal.
Let's see, we have: sqrt(73) + sqrt(29) = sqrt(194)
which means:
73 + 29 + 2*sqrt(73*29) = 194
2*sqrt(2117) = 194 - 102
2*sqrt(2117) = 92
sqrt(2117) = 46 which is NOT true. Since 46^2 = 2116, sqrt(2117) would be a little higher and NOT equal.
Therefore, those shapes do not form a triangle, but a four-sided shape (how is it called in English?  )
____________
|
|
TheDeath
Responsible
Undefeatable Hero
with serious business
|
|
posted November 10, 2008 03:30 PM |
|
|
I know that may be true, but I don't understand why, because both the red and the yellow components have the same "direction" of hypotenuse right? Or is the first triangle not a triangle either?
____________
The above post is subject to SIRIOUSness.
No jokes were harmed during the making of this signature.
|
|
Asheera
Honorable
Undefeatable Hero
Elite Assassin
|
|
posted November 10, 2008 03:31 PM |
|
|
Red = triangle
Yellow = triangle
The whole shape together = NOT triangle 
____________
|
|
dimis
Responsible
Supreme Hero
Digitally signed by FoG
|
|
posted November 10, 2008 03:33 PM |
|
Edited by dimis at 15:34, 10 Nov 2008.
|
Quote:
You could look here for a start, although it doesn't have all the participants in this thread I think...
Thanks. I 'll have a look when I get home and post who are the ones that are missing.
Quote:
... both the red and the yellow components have the same "direction" of hypotenuse right?
Nope. Check again. There is an easy check for that by actual counting.
____________
The empty set
|
|
TheDeath
Responsible
Undefeatable Hero
with serious business
|
|
posted November 10, 2008 03:39 PM |
|
|
Yeah, I got it, thanks guys
____________
The above post is subject to SIRIOUSness.
No jokes were harmed during the making of this signature.
|
|
Ecoris
Promising
Supreme Hero
|
|
posted November 10, 2008 04:10 PM |
|
Edited by Ecoris at 16:10, 10 Nov 2008.
|
Quote:
If you multiply the first one hundred numbers together 1 * 2 * 3 *...* 100, you'll get the first number of Ecoris' series, because any number within the next 100 numbers will be guarenteed to be a multiple of one of the first 100 numbers.
This is close, but 100!+1 is in fact not divisible by any of the numbers 2,3,4,...,100. Can you fix this?
Quote:
There's another 100 consecutive numbers much smaller than that though.
And here's another question, is there a way to prove that there's no 100 consecutive numbers smaller than that second series?(the one that I didn't give an answer to)
I'm not sure what you mean. Are we considering the "smallest" such sequence, i.e. the smallest n for which none of the numbers n,n+1,n+2,...,n+99 are primes?
____________
|
|
dimis
Responsible
Supreme Hero
Digitally signed by FoG
|
|
posted November 10, 2008 05:03 PM |
|
|
I would be interested in finding such a bound. Once I gave a variation of this problem as a programming lab-assignment, but I don't think I had a lower bound on the sequence of the required length.
My observation though, is that the sequence you are looking for is actually a proper subsequence of a bigger one; i.e. in a sense, you can not find exactly 100 consecutive numbers of the form you are looking for. I don't know if I make sense here though ... Any guesses?
____________
The empty set
|
|
Ecoris
Promising
Supreme Hero
|
|
posted November 10, 2008 05:17 PM |
|
Edited by Ecoris at 17:19, 10 Nov 2008.
|
Quote:
I would be interested in finding such a bound.
The n I referred to just above?
Quote:
My observation though, is that the sequence you are looking for is actually a proper subsequence of a bigger one; i.e. in a sense, you can not find exactly 100 consecutive numbers of the form you are looking for. I don't know if I make sense here though ... Any guesses?
If for some n none of the numbers n,n+1,n+2,...,n+99 are primes, then either n-1 or n+100 is even since their parities differ. Clearly n-1 =/= 2 since otherwise n = 3 which is a prime. Hence n-1 or n+100 is not a prime.
So you can't find such a sequence for which both n-1 and n+100 are primes. 100 was just an arbitrary natural number; it could have been any other.
____________
|
|
dimis
Responsible
Supreme Hero
Digitally signed by FoG
|
|
posted November 10, 2008 05:25 PM |
|
|
Quote:
The n I referred to just above?
Yes.
And yes on your answer! Every such sequence of consecutive numbers appears between primes, and all primes >= 3 are odd. So, the sequence of first 100 such consecutive numbers will appear when the first sequence of 101 will be revealed, which is from 1444310 to 1444410.
____________
The empty set
|
|
TheDeath
Responsible
Undefeatable Hero
with serious business
|
|
posted November 10, 2008 05:34 PM |
|
Edited by TheDeath at 17:40, 10 Nov 2008.
|
Quote:
Find 100 consecutive numbers containing no primes.
370262, 370263.... 370362 is the smallest
I did it with Pari, so check your results against this
Here's the script:Quote:
out = 0; j = 103; i = 28;
while(1, if((prime(i) - j) > 100, out = j; break, j = prime(i); i++))
this gives the prime, which has more than 100 difference between this prime and the next prime. In this case it gives 370261, so we add '1' to get the smallest consecutive sequence of 100 non-primes
I still have no clue how to do this without the above brute-force method.
____________
The above post is subject to SIRIOUSness.
No jokes were harmed during the making of this signature.
|
|
dimis
Responsible
Supreme Hero
Digitally signed by FoG
|
|
posted November 10, 2008 05:58 PM |
|
|
You are right; I was confused with the variation I was working on that other problem. The fact that I know where the first 101-consecutive numbers lie, doesn't mean that I know where the first 100-consecutive numbers lie. I just know an upper bound on my search.
Thanks for pointing that out.
|
|
friendofgunnar
Honorable
Legendary Hero
able to speed up time
|
|
posted November 10, 2008 08:37 PM |
|
|
Ecoris: Quote:
This is close, but 100!+1 is in fact not divisible by any of the numbers 2,3,4,...,100. Can you fix this?
I think 101! + 2,101! + 3....101! + 101 should yield a one-hundred number sequence.
The smaller sequence I was thinking of was if you multiply all of the prime numbers between 1 and 100 101 together, you will find another chain of 100 prime-free numbers. The reason is that every number between 1 and 101 is either a prime or a multiple of one of those primes. Thus every number in the smaller sequence will either be a multiple of one of the primes between 1 and 101, or it will be a multiple of a multiple of one of the primes between 1 and 101.
It's much bigger than the ones discussed already in this thread of course ;p
|
|
Ecoris
Promising
Supreme Hero
|
|
posted November 10, 2008 11:15 PM |
|
|
Quote:
I think 101! + 2,101! + 3....101! + 101 should yield a one-hundred number sequence.
Exactly. This is the simplest way to prove the existence of such a sequence.
(The argument holds in general, of course. It means that there are arbitrary long "sections" on the line of natural numbers that contain no primes).
____________
|
|
dimis
Responsible
Supreme Hero
Digitally signed by FoG
|
posted November 11, 2008 05:18 PM |
|
|
Birthdays missing
Ok,
It was a very long day yesterday so here's a post related to birthdays.
I don't know the dates for the following people:
* Celfious
* JollyJoker
* Gnoll_Mage
* Domzilla
* JoonasTo
* homm3megejas
* Keldorn
Can you please IM me your birthdays?
If you feel weird to share such info with me, I can make the first step.
Mine is on April 13.
____________
The empty set
|
|
Asheera
Honorable
Undefeatable Hero
Elite Assassin
|
|
posted November 11, 2008 08:35 PM |
|
|
After you have those birthdays can you send me a HCM with them or post them in the birthday thread so I can add them? Unless somebody minds, of course...
____________
|
|
dimis
Responsible
Supreme Hero
Digitally signed by FoG
|
|
posted November 11, 2008 11:11 PM |
|
|
I am NOT going to post *any* birthday to *any* thread.
I just posted mine to motivate others to send me an IM.
____________
The empty set
|
|
broadstrong
Promising
Known Hero
Level 20 Vassal of Light
|
|
posted November 12, 2008 01:58 AM |
|
|
Quote:
Factor the number into primes. It would be easy then to determine whether a given number is divided by all, or some, of the numbers you listed.
@Corribus,
Great answer, I had not even initially thought about this, as I am merely asking on divisibility tests.
Quote:
Ah, that's easy.
2: if it's an even number
3: if the checksum can be divided by 3
4: if the last two digits can be divided by 4 (i.e. 124
5: if the number ends on 5 or 0
6: if the numver can be divided by 2 AND 3
9: if the checksum can be divided by 9
10: if the number ends on a 0
11: if the double-digit checksum can be divided by 11.
@JJ,
I don't know what you exactly mean by "checksum", but I guess you got the idea.
Anyone knows how to increase the percentage of getting required abilities? I know that some abilities are very difficult to get them to appear (guardian angel is one good example, because there are juz too many competing abilities like suppress light and eternal light that will also appear in the choices; I reckon some abilities in sorcery and dark magic also face the same issues)
____________
The queer part of the Carcity/Broadstrong/Zamfir[
/b] threeway, equipped with sailing, summon allies, spatial travel and supermover.
Many current projects on hand.
|
|
|
|
This thread is pages long: 
